B3: Generate State $\bigotimes_i\lparen\cos{T_i}\ket{0}+\sin{T_i}\ket{1}\rparen$

Editorial

To implement the solution, we need to prepare the state $\cos T_i\ket{0} + \sin T_i\ket{1}$ from $\ket{0}$ independently for each qubit.

Here, when the $Ry(\theta)$ gate is applied to $\ket{0}$, it results in the state $\cos\frac{\theta}{2}\ket{0} + \sin\frac{\theta}{2}\ket{1}$.

Therefore, by setting $\theta = 2T_i$ and applying the $Ry(\theta)$ gate to each qubit, we can solve this problem.

For the case where $n = 3$ and $(T_0, T_1, T_2) = (\pi / 6, \pi / 3, \pi / 2)$, the circuit diagram is shown below.

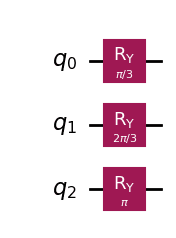
Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve(n: int, T: list[float]) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        qc.ry(T[i] * 2, i)
 
    return qc