A2: Qubit Swap

Editorial

A quantum gate that swaps the states of qubits is called a swap gate.

In this problem, since only the qubits are swapped and the probability amplitudes remain unchanged, you might consider using an $X$ gate or a $CX$ gate ¹.

In fact, it is known that the swap gate can be implemented using three controlled $X$ gates, as shown below:

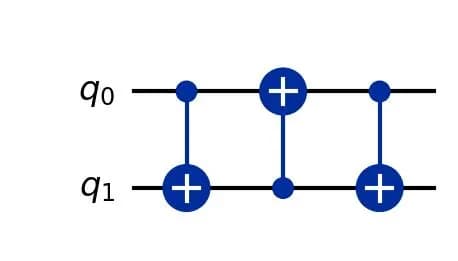
The state transitions can be expressed as follows:

The $CX(0, 1)$ gate swaps the probability amplitudes of $\ket{10}$ and $\ket{11}$, while the $CX(1, 0)$ gate swaps the probability amplitudes of $\ket{01}$ and $\ket{11}$.

The circuit depth is $3$.

Follow-up

XOR swap is a classical algorithm to swap $2$ variables $x$ and $y$ in $3$ steps. This algorithm uses XOR operations to achieve swapping in the following $3$ steps:

1. Replace $y$ with $x + y \pmod 2$.
2. Replace $x$ with $x + y \pmod 2$.
3. Replace $y$ with $x + y \pmod 2$.

The operation of replacing $y$ with $x + y \pmod 2$ corresponds to $CX(0, 1)$, and the operation of replacing $x$ with $x + y \pmod 2$ corresponds to $CX(1, 0)$, so you can solve this problem based on this algorithm.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve() -> QuantumCircuit:
    qc = QuantumCircuit(2)
 
    qc.cx(0, 1)
    qc.cx(1, 0)
    qc.cx(0, 1)
 
    return qc