A2: Controlled Gate I

Editorial

The goal is to construct a quantum circuit that applies a Hadamard gate $H$ to $\ket{m}$, conditioned on $\ket{k}_n = \ket{00 ... 0}_n$.

So, how can we apply a Hadamard gate $H$ to $\ket{m}$ only when $\ket{k}_n = \ket{00 ... 0}_n$?

You can achieve this by performing the following steps in order.

• Step 1: Apply an $X$ gate to each qubit in $\ket{k}_n = \ket{k_0 k_1 ... k_{n - 1}}_n$.
• Step 2: Apply a multi-controlled Hadamard gate¹ with $\ket{k_0 k_1 ... k_{n - 1}}_n$ as the control qubits and $\ket{m}$ as the target qubit.
• Step 3: Apply the inverse of Step 1 to restore $\ket{k}_n$ to its original state.

Therefore, when $\ket{k}_n = \ket{00 ... 0}_n$, the following state transitions hold:

As a result, you can solve this problem by following these steps.

The circuit diagram for $n = 3$ is as follows.

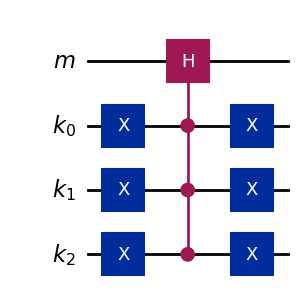
The circuit depth is $3$.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit, QuantumRegister
from qiskit.circuit.library import HGate
 
 
def solve(n: int) -> QuantumCircuit:
    m, k = QuantumRegister(1), QuantumRegister(n)
    qc = QuantumCircuit(m, k)
 
    qc.x(k)
 
    qc.compose(HGate().control(len(k)), [*k, m[0]], inplace=True)
 
    qc.x(k)
 
    return qc

The control gate is usually enabled when the control bit is set to $1$, but $0$ can also be used.

from qiskit import QuantumCircuit, QuantumRegister
from qiskit.circuit.library import HGate
 
 
def solve(n: int) -> QuantumCircuit:
    m, k = QuantumRegister(1), QuantumRegister(n)
    qc = QuantumCircuit(m, k)
 
    qc.compose(HGate().control(len(k), ctrl_state=0), [*k, m[0]], inplace=True)
 
    return qc