A3: Controlled Gate II

Editorial

The goal is to construct a quantum circuit that applies an $X$ gate to $\ket{m}$, conditioned on $\ket{k}_n \neq \ket{00 ... 0}_n$.

Based on the solution to Problem A2, it seems possible to apply an $X$ gate to $\ket{m}$ only when $\ket{k}_n = \ket{00 ... 0}_n$.

So, we consider a method where we apply the $X$ gate twice when $\ket{k}_n = \ket{00 ... 0}_n$, and once when $\ket{k}_n \neq \ket{00 ... 0}_n$.

You can achieve this by performing the following steps in order.

• Step 1: Apply an $X$ gate to $\ket{m}$.
• Step 2: Apply an $X$ gate to $\ket{m}$ only when $\ket{k}_n = \ket{00 ... 0}_n$, using the same method as in Problem A2.

Therefore, when $\ket{k}_n = \ket{00 ... 0}_n$, the following state transitions hold by using the fact that $XX = I$:

As a result, you can solve this problem by following these steps.

The circuit diagram for $n = 3$ is as follows.

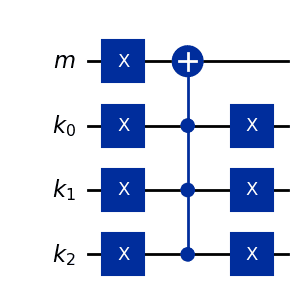
The circuit depth is $3$.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit, QuantumRegister
from qiskit.circuit.library import XGate
 
 
def solve(n: int) -> QuantumCircuit:
    m, k = QuantumRegister(1), QuantumRegister(n)
    qc = QuantumCircuit(m, k)
 
    qc.x(m[0])
 
    qc.x(k)
 
    qc.compose(XGate().control(len(k)), [*k, m[0]], inplace=True)
 
    qc.x(k)
 
    return qc