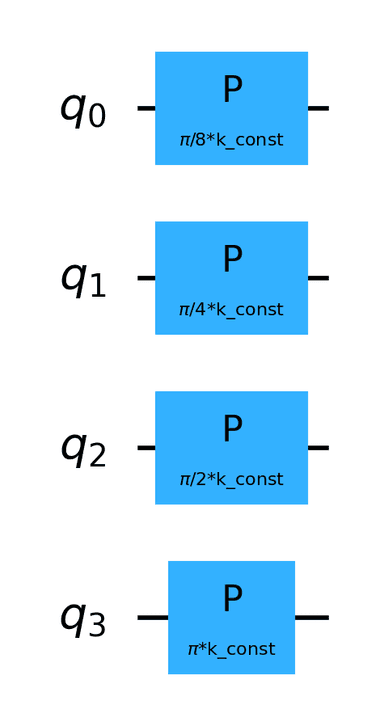QCoder

Editorial

For general $n$ , you can solve this problem by appropriately transforming the expressions.

By expressing $\ket{a}$ as $\ket{a_0} \ket{a_1} ... \ket{a_{n - 1}}$ where $a_i \in \lbrace 0, 1 \rbrace$ , the following transformation holds:

\begin{align} \mathrm{QFT}(k') &= \frac{1}{\sqrt{2^n}} \sum_{0 \leq a < 2^n} \omega^{a k'} \ket{a} \\ &= \frac{1}{\sqrt{2^n}} \sum_{0 \leq a < 2^n} \omega^{a (k + k_{const})} \ket{a} \\ &= \frac{1}{\sqrt{2^n}} \sum_{0 \leq a < 2^n} \omega^{(a_0 + 2 a_1 + ... + 2^{n - 1}) k_{const}} \omega^{ak} \ket{a_0} \ket{a_1} ... \ket{a_{n - 1}} \\ &= \frac{1}{\sqrt{2^n}} \sum_{0 \leq a < 2^n} \omega^{k_{const} a_0} \omega^{(2 k_{const}) a_1} ... \omega^{(2^{n - 1} k_{const}) a_{n - 1}} \omega^{a k} \ket{a_0} \ket{a_1} ... \ket{a_{n - 1}} \\ &= \frac{1}{\sqrt{2^n}} \sum_{0 \leq a < 2^n} \omega^{a k} \omega^{k_{const} a_0} \ket{a_0} \omega^{(2 k_{const}) a_1} \ket{a_1} ... \ \omega^{(2^{n - 1} k_{const}) a_{n - 1}} \ket{a_{n - 1}} \\ &= \frac{1}{\sqrt{2^n}} \sum_{0 \leq a < 2^n} \omega^{a k} P\left(\frac{2 \pi}{2^n} k_{const} \right) \ket{a_0} P\left(\frac{2 \pi}{2^n} 2k_{const} \right) \ket{a_1} ... \ P\left(\frac{2 \pi}{2^n} 2^{n - 1}k_{const} \right) \ket{a_{n - 1}} \\ &= P\left(\frac{2 \pi}{2^n} k_{const} \right) \otimes P\left(\frac{2 \pi}{2^n} 2k_{const} \right) \otimes ... \otimes P\left(\frac{2 \pi}{2^n} 2^{n - 1}k_{const} \right) \frac{1}{\sqrt{2^n}} \sum_{0 \leq a < 2^n} \omega^{a k} \ket{a} \\ &= P\left(\frac{2 \pi}{2^n} k_{const} \right) \otimes P\left(\frac{2 \pi}{2^n} 2k_{const} \right) \otimes ... \otimes P\left(\frac{2 \pi}{2^n} 2^{n - 1}k_{const} \right) \mathrm{QFT}(k). \end{align}

Therefore, by applying the phase shift gate $P(\theta_i)$ with rotation angle

\begin{equation} \theta_i = \frac{2 \pi}{2^n} \cdot 2^i \cdot k_{const} \end{equation}

to the $i$ -th qubit, we can obtain the desired quantum state.

The circuit diagram for $n = 4$ is as follows.

The circuit depth is $1$ .

Sample Code

Below is a sample program:

import math
 
from qiskit import QuantumCircuit
 
 
def solve(n: int, k_const: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        theta = (2 * math.pi / 2 ** n) * (2 ** i) * k_const
        qc.p(theta, i)
 
    return qc

B1: Action in the Fourier Basis

Editorial

Sample Code