LogoQCoder Programming Contest 005
Sign in
← Previous ProblemNext Problem →

A5: Minus Oracle

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 400

Writer: PSL

Editorial

By flipping all qubits, you can gain a clearer perspective on this problem.

In other words, by applying an XX gate to every qubit, we obtain

∣k⟩→X⊗X⊗ ... ⊗X∣j⟩.\begin{equation} \ket{k} \xrightarrow{X \otimes X \otimes \ ... \ \otimes X} \ket{j}. \end{equation}

In this case, since each bit of k+jk + j becomes 11, we have k+j=2n−1k + j = 2^n - 1.

Therefore, the transformation can be rewritten as

∣k⟩→X⊗X⊗ ... ⊗X∣2n−1−k⟩.\begin{equation} \ket{k} \xrightarrow{X \otimes X \otimes \ ... \ \otimes X} \ket{2^n - 1 - k}. \end{equation}

You can solve this problem by applying an oracle that adds +1 (mod 2n)+ 1 \ (\text{mod} \ 2^n) to the quantum state. For details on how to implement this oracle, see the QPC004 A5 Editorial.

The circuit diagram for n=4n = 4 is as follows.

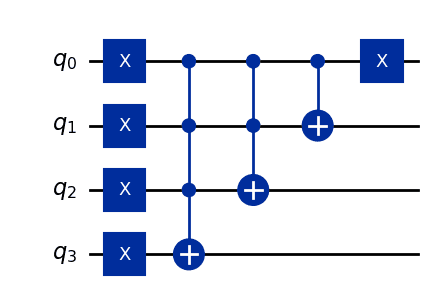
The circuit depth is n+1n + 1.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(range(n))
 
    for i in reversed(range(1, n)):
        qc.mcx(list(range(i)), i)
 
    qc.x(0)
 
    return qc