A4: Cyclic Shift Oracle III

Editorial

You can solve this problem by effectively using the Swap gate.

Let $L = n + 1$. You can obtain the desired quantum state by performing the following steps in order.

• Step 1: For $j = 0, 2, 4, ... \left( < L - 1 \right)$, swap the $j$ th and $(j + 1)$ th qubits.
• Step 2: For $j = 0, 4, 8, ... \left( < L - 2 \right)$, swap the $j$ th and $(j + 2)$ th qubits.
• Step 3: For $j = 0, 8, 16, ... \left( < L - 4 \right)$, swap the $j$ th and $(j + 4)$ th qubits.

Therefore, when $n = 4$, letting $\ket{k}_4 = \ket{k_0 k_1 k_2 k_3}_4$, the following state transitions hold:

As a result, you can solve this problem by following these steps.

The circuit diagram for $n = 4$ is as follows.

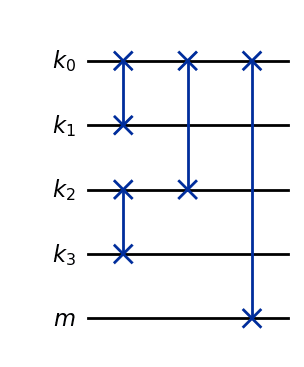
Each step has circuit depth $1$, so the total circuit depth is $\log_2 n$.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    L = n + 1
    qc = QuantumCircuit(L)
 
    for i in range(L.bit_length()):
        for j in range(0, L - (2 ** i), 2 ** (i + 1)):
            qc.swap(j, j + (2 ** i))
 
    return qc