A2: Controlled Gate I

解説

$\ket{k}_n = \ket{00 ... 0}_n$ のときのみ、$\ket{m}$ にアダマールゲート $H$ を作用させる量子回路を実装する問題です。

では、重ね合わせ状態の中の特定の計算基底状態 $\ket{k}_n = \ket{00 ... 0}_n$ のときのみ、$\ket{m}$ にアダマールゲート $H$ を作用させるにはどうすれば良いでしょうか？

これは次の操作を順に行うことによって実現できます。

• 操作 1 : $\ket{k}_n = \ket{k_0 k_1 ... k_{n - 1}}_n$ の全ての量子ビットに対して $X$ ゲートを作用させる。
• 操作 2 : $\ket{k_0 k_1 ... k_{n - 1}}_n$ を制御ビット、$\ket{m}$ を標的ビットとする複数制御アダマールゲート¹を作用させる。
• 操作 3 : 操作 1 の逆操作を行い、$\ket{k}_n$ を元の状態に戻す。

よって、$\ket{k}_n = \ket{00 ... 0}_n$のとき

という状態遷移が成り立つため、この問題を解くことができます。

$n = 3$ の場合の量子回路は次のように表されます。

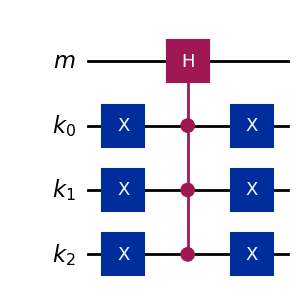
回路の深さは $3$ です。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit, QuantumRegister
from qiskit.circuit.library import HGate
 
 
def solve(n: int) -> QuantumCircuit:
    m, k = QuantumRegister(1), QuantumRegister(n)
    qc = QuantumCircuit(m, k)
 
    qc.x(k)
 
    qc.compose(HGate().control(len(k)), [*k, m[0]], inplace=True)
 
    qc.x(k)
 
    return qc

通常、制御ビットは $1$ で制御を行いますが、次のように $0$ を使って制御する方法で記述することもできます。

from qiskit import QuantumCircuit, QuantumRegister
from qiskit.circuit.library import HGate
 
 
def solve(n: int) -> QuantumCircuit:
    m, k = QuantumRegister(1), QuantumRegister(n)
    qc = QuantumCircuit(m, k)
 
    qc.compose(HGate().control(len(k), ctrl_state=0), [*k, m[0]], inplace=True)
 
    return qc