LogoQCoder Programming Contest 005
ログイン
← 前の解説次の解説 →

A3: Controlled Gate II

実行時間制限：3 秒

メモリ制限：512 MiB

配点：200点

Writer：PSL

解説

∣k⟩n≠∣00...0⟩n\ket{k}_n \neq \ket{00 ... 0}_n のときのみ、∣m⟩\ket{m} に XX ゲートを作用させる量子回路を実装する問題です。

問題 A2 の解答を思い出すと、∣k⟩n=∣00...0⟩n\ket{k}_n = \ket{00 ... 0}_n のときのみ、∣m⟩\ket{m} に XX ゲートを作用させることはできそうです。

では、∣k⟩n=∣00...0⟩n\ket{k}_n = \ket{00 ... 0}_n ときは、XX ゲートを 22 回作用させ、∣k⟩n≠∣00...0⟩n\ket{k}_n \neq \ket{00 ... 0}_n のときは XX ゲートを 11 回作用させる方法を考えましょう。

これは次の操作を順に行うことによって実現できます。

  • 操作 1 : ∣m⟩\ket{m} に XX ゲートを作用させる。
  • 操作 2 : ∣k⟩n=∣00...0⟩n\ket{k}_n = \ket{00 ... 0}_n のときのみ、∣m⟩\ket{m} に XX ゲートを作用させる。（問題 A2 と同様の方法）

よって、∣k⟩n=∣00...0⟩n\ket{k}_n = \ket{00 ... 0}_nのとき XX=IXX = I を利用すると

∣m⟩∣00...0⟩n→操作 1 X∣m⟩∣00...0⟩n→操作 2 XX∣m⟩∣00...0⟩n=∣m⟩∣00...0⟩n\begin{align} \ket{m}\ket{00 ... 0}_n \xrightarrow{\text{操作 1 }} &X \ket{m}\ket{00 ... 0}_n \\ \xrightarrow{\text{操作 2 }} &X X \ket{m}\ket{00 ... 0}_n \\ = &\ket{m}\ket{00 ... 0}_n \end{align}

という状態遷移が成り立つため、この問題を解くことができます。

n=3n = 3 の場合の量子回路は次のように表されます。

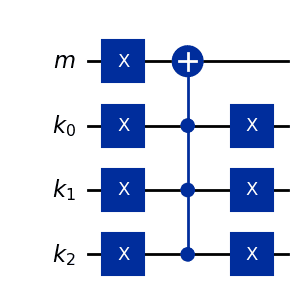
回路の深さは 33 です。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit, QuantumRegister
from qiskit.circuit.library import XGate
 
 
def solve(n: int) -> QuantumCircuit:
    m, k = QuantumRegister(1), QuantumRegister(n)
    qc = QuantumCircuit(m, k)
 
    qc.x(m[0])
 
    qc.x(k)
 
    qc.compose(XGate().control(len(k)), [*k, m[0]], inplace=True)
 
    qc.x(k)
 
    return qc