A4: Cyclic Shift Oracle III

解説

スワップゲートをうまく利用することで、この問題を解くことができます。

$L = n + 1$ とするとき、次の操作を順に行うことによって目的の量子状態を実現できます。

• 操作 1 : $j = 0, 2, 4, ... \left( < L - 1 \right)$ に対し、$j$ 番目と $j + 1$ 番目をスワップする。
• 操作 2 : $j = 0, 4, 8, ... \left( < L - 2 \right)$ に対し、$j$ 番目と $j + 2$ 番目をスワップする。
• 操作 3 : $j = 0, 8, 16, ... \left( < L - 4 \right)$ に対し、$j$ 番目と $j + 4$ 番目をスワップする。

よって $n = 4$ のとき、$\ket{k}_4 = \ket{k_0 k_1 k_2 k_3}_4$とすると

という状態遷移が成り立つため、この問題を解くことができます。

$n = 4$ の場合の量子回路は次のように表されます。

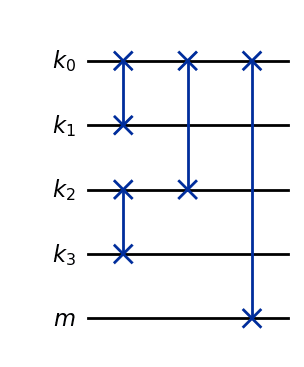
各操作の回路の深さは $1$ となるため、回路全体の深さは $\log_2 n$ です。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    L = n + 1
    qc = QuantumCircuit(L)
 
    for i in range(L.bit_length()):
        for j in range(0, L - (2 ** i), 2 ** (i + 1)):
            qc.swap(j, j + (2 ** i))
 
    return qc