LogoQCoder Programming Contest 005
ログイン
← 前の解説次の解説 →

A5: Minus Oracle

実行時間制限：3 秒

メモリ制限：512 MiB

配点：400点

Writer：PSL

解説

全ての量子ビットを反転させることによって、問題の見通しが良くなります。

すなわち、全ての量子ビットに対して XX ゲートを作用させると

∣k⟩→X⊗X⊗ ... ⊗X∣j⟩\begin{equation} \ket{k} \xrightarrow{X \otimes X \otimes \ ... \ \otimes X} \ket{j} \end{equation}

となります。このとき、k+jk + j は全てのビットが 11 となるので、k+j=2n−1k + j = 2^n - 1 が成り立ちます。 よって、

∣k⟩→X⊗X⊗ ... ⊗X∣2n−1−k⟩\begin{equation} \ket{k} \xrightarrow{X \otimes X \otimes \ ... \ \otimes X} \ket{2^n - 1 - k} \end{equation}

のように書き換えられます。

この量子状態に対して +1 (mod 2n)+ 1 \ (\text{mod} \ 2^n) をするようなオラクルを作用させることによって、この問題を解くことができます。 詳しいオラクルの実装については、QPC004 A5 解説を参照してください。

n=4n = 4 の場合の量子回路は以下の通りです。

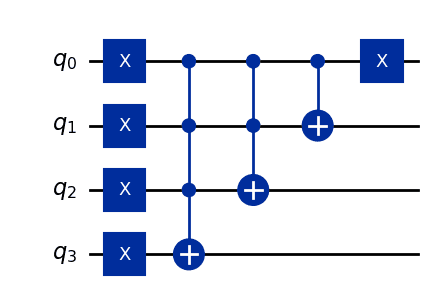
回路の深さは n+1n + 1 です。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(range(n))
 
    for i in reversed(range(1, n)):
        qc.mcx(list(range(i)), i)
 
    qc.x(0)
 
    return qc